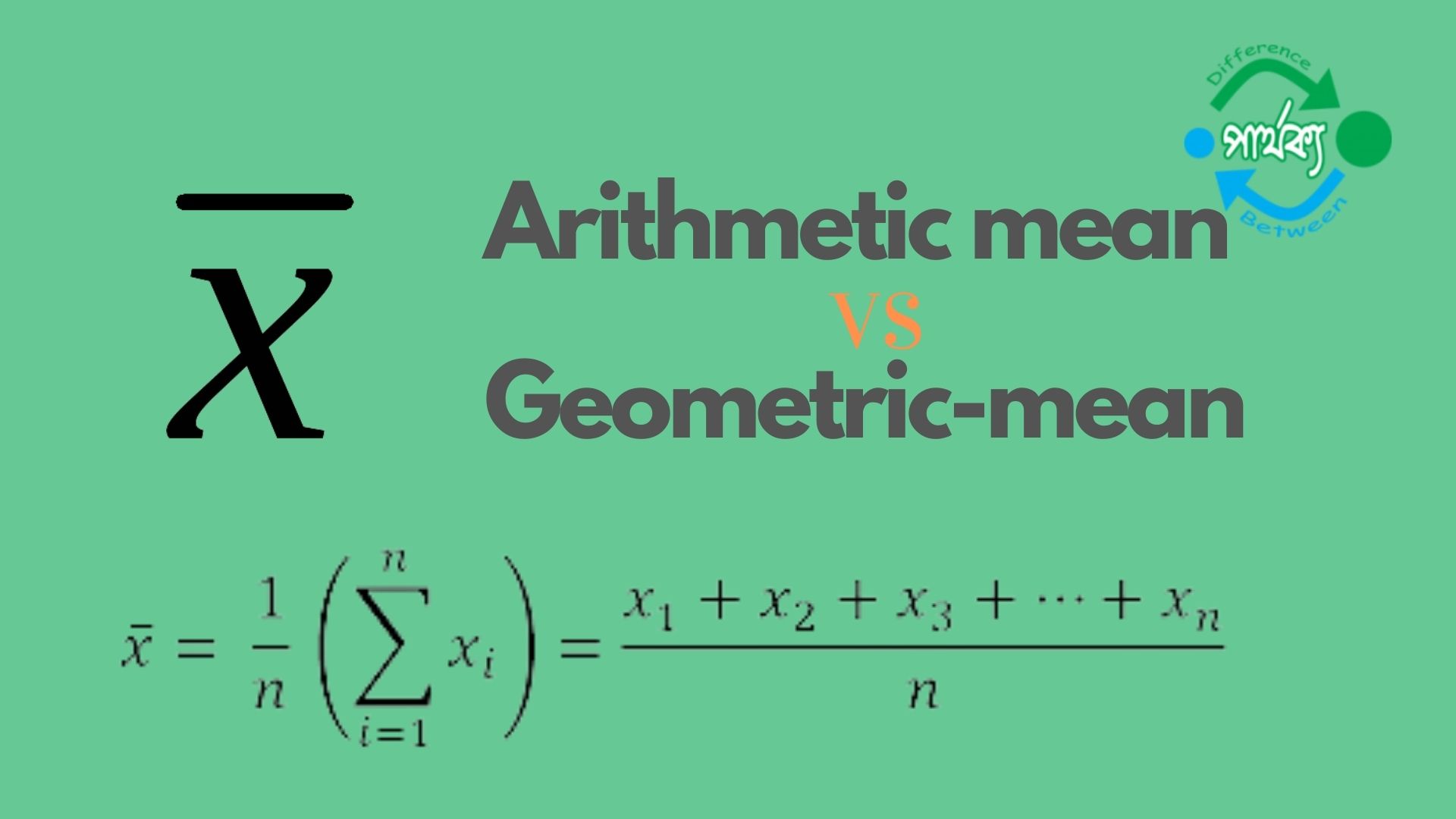গাণিতিক গড় (Arithmatic Mean):
পাঠ্যপুস্তকে গণিতেই আপনারা গাণিতিক গড়ের সাথে পরিচিত হয়েছেন। প্রাপ্ত মান গুলোর যোগফল বা সমষ্টিকে তাদের সংখ্যা দ্বারা ভাগ করলে গাণিতিক গড় (বা সংক্ষেপে গড়) পাওয়া যাবে। প্রাপ্ত মান গুলোর যে একক (Unit) থাকে গড়ের এককও তাই হয়। ধরা যাক, x চলকটির (অশ্রেণীকৃত) x1, x2, x3 …………….xn মান আছে। গাণিতিক গড়কে যদি X দ্বারা সূচিত করা হয়।
x̅ = Error!= 1nn∑i=1Xi; i = 1, 2, 3, …………… n.
জ্যামিতিক গড় (Geometric Mean):
কোন চলকের n সংখ্যক অশূন্য ধনাত্মক মান গুলোর গুণফলের nতম মূল হচ্ছে ঐ মান গুলোর জ্যামিতিক গড়। ধরা যাক X চলকের (অশ্রেণীকৃত) n সংখ্যক মান x1, x2, x3 …………….xn এদের সবাই ধনাত্মক এবং কোনটিই শূন্য নয়। এক্ষেত্রে জ্যামিতিক গড় হবে- G.M = (XError! ´ XError! ´ …………. ´ Xn) 1/n
গাণিতিক গড় ও জ্যামিতিক গড়ের মধ্যে পার্থক্যঃ
প্রাপ্ত মান গুলোর যোগফল বা সমষ্টিকে তাদের সংখ্যা দ্বারা ভাগ করলে গাণিতিক গড় পাওয়া যায়। গাণিতিক গড় ও জ্যামিতিক গড়ের মধ্যে পার্থক্য নিম্নরূপ-
১। আমাদের দৈনন্দিন জীবনে কোন দ্রব্যের গড় ক্রয়মূল্য, মাসিক গড় আয়, শিল্প পণ্যের গড় চাহিদা ইত্যাদির ক্ষেত্রে গাণিতিক গড় ব্যবহৃত হয় কারণ এটা সহজে হিসাব করা যায়। অন্যদিকে, জ্যামিতিক গড়ের সূত্র সহজে বুঝা কঠিন। গণিতের বিশেষ জ্ঞান না থাকলে এটা নির্ণয় করা কঠিন।
২। তথ্যসমূহের প্রত্যেকটির প্রকৃত মান দেয়া না থাকলে এবং কেবলমাত্র এর সমষ্টি এবং সংখ্যা জানা থাকলেই গাণিতিক গড় নির্ণয় করা যায়। অন্যদিকে, তথ্যমানের কোন একটি মান শূন্য হলে জ্যামিতিক গড় নির্ণয় করা যায় না।
৩। নমুনার তারতম্য হলেও গাণিতিক গড় কম প্রভাবিত হয়। অন্যদিকে, তথ্যমানের কোন একটি মান ঋণাত্মক হলে জ্যামিতিক গড় নির্ণয় করা যায় না।