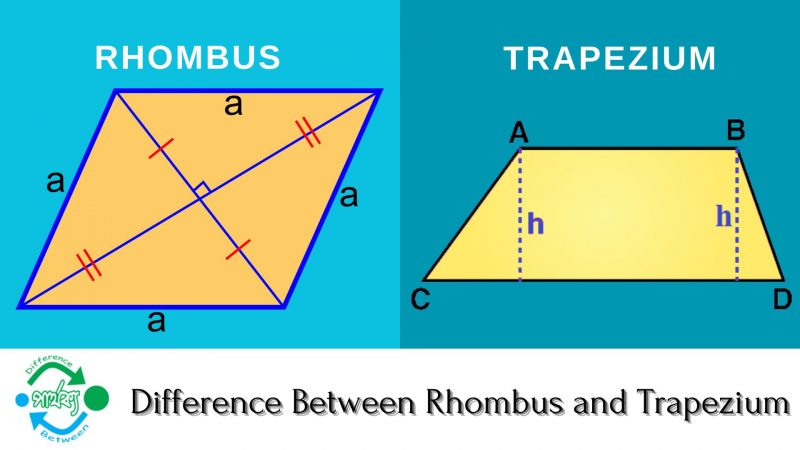
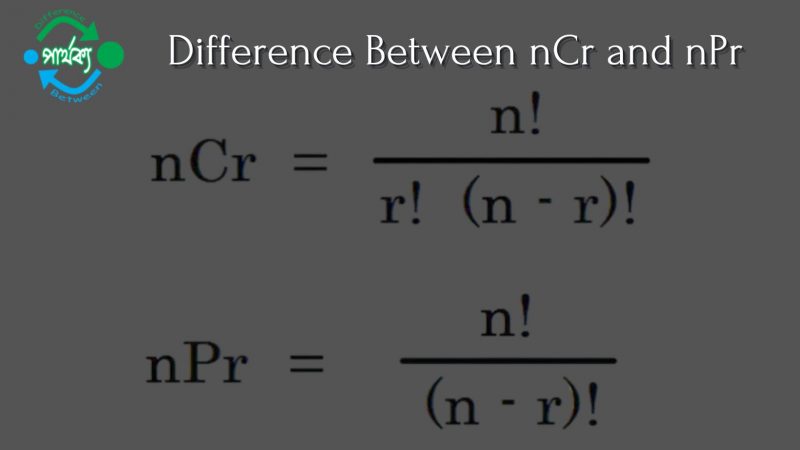জ্যামিতিক হার (Geometric Mean) :
জ্যামিতিক হার হলো একটি মৌলিক অংশের সংখ্যাগুলির গুণফলের মাধ্যমিক মূলবিন্যাস। অন্যভাবে বলতে গেলে, একটি ডেটা সেটের সবগুলি মৌলিক ঘটকের সাধারণ গুণফলের মাধ্যমিক মূলবিন্যাসকে জ্যামিতিক হার বলা হয়। যখন আপনি একটি ডেটা সেটের মৌলিক ঘটকগুলির গুণফল বের করেন এবং তাদের সংখ্যা সমান হয়, তখন আপনি সেই মৌলিক ঘটকগুলির জ্যামিতিক হার পেতেন। এই মৌলিক ঘটকগুলির গুণফলের মাধ্যমিক মূলবিন্যাসই জ্যামিতিক হার।
উদাহরণঃ ধরা যাক, আপনার একটি ডেটা সেট হয় [2, 4, 8]। তাহলে জ্যামিতিক হার বের করার জন্য আপনি মৌলিক ঘটকগুলির গুণফল নিবেন এবং সেটে থাকা মৌলিক ঘটকের সংখ্যা সংখ্যাগুলির সমমান হলে তাদের জ্যামিতিক হার পেতেন:
জ্যামিতিক হার = √(2 × 4 × 8) = √64 = 8
এখানে, মৌলিক ঘটকগুলির গুণফল হচ্ছে 64 এবং তাদের সংখ্যা সমমান, তাহলে জ্যামিতিক হার হল 8।
গাণিতিক হার (Arithmetic Mean) :
গাণিতিক হার হলো একটি ডেটা সেটের সমস্ত মানের যোগফল এবং তাদের সংখ্যা দ্বারা ভাগ করা মাধ্যমিক মান। অন্য ভাবে বলতে, একটি ডেটা সেটের সবগুলি মানের যোগফল তাদের সংখ্যা দ্বারা ভাগ করা হয় এবং সেই মাধ্যমিক মানটি গাণিতিক হার হয়। গাণিতিক হার ক্যালকুলেট করার জন্য, আপনি সেটের সবগুলি মানের যোগফল করে সংখ্যা দ্বারা ভাগ করেন। এটি ডেটা সেটের সাধারণ ত্রুটি নির্দেশ করার জন্য ব্যবহৃত হয়, যেটি তারমূলে উপস্থিত মৌলিক ঘটকের মাধ্যমে প্রভাবিত হয় না।
উদাহরণঃ ধরা যাক, আপনার একটি ডেটা সেট হয় [5, 10, 15, 20]। তাহলে গাণিতিক হার বের করার জন্য আপনি সবগুলি মানের যোগফল করেন এবং সেটে থাকা মানের সংখ্যা দ্বারা ভাগ করেন:
গাণিতিক হার = (5 + 10 + 15 + 20) / 4 = 50 / 4 = 12.5
এখানে, সমস্ত মানের যোগফল হচ্ছে 50 এবং তাদের সংখ্যা দ্বারা ভাগ করা হলে গাণিতিক হার হল 12.5।
জ্যামিতিক হার ও গাণিতিক হারের মধ্যে পার্থক্যঃ
জ্যামিতিক হার ও গাণিতিক হার বিষয় দুটি এক মনে হলেও এদের মধ্যে পার্থক্য বিদ্যমান। তাই নিচে জ্যামিতিক হার ও গাণিতিক হারের মধ্যে পার্থক্য দেখানো হয়েছে-
১. জ্যামিতিক হার হলো একটি মৌলিক অংশের সংখ্যাগুলির গুণফলের মাধ্যমিক মূলবিন্যাস। অন্যদিকে, গাণিতিক হার হলো একটি ডেটা সেটের সমস্ত মানের যোগফল এবং তাদের সংখ্যা দ্বারা ভাগ করা মাধ্যমিক মান।
২. জ্যামিতিক হার হচ্ছে কোন কিছু দ্বিগুণ হারে বৃদ্ধি পাওয়াকে বোঝায়। অন্যদিকে, গাণিতিক হার হলো কোন কিছু ক্রমান্বয়ে বৃদ্ধি পাওয়া।
৩. ম্যালথাসের মতে, জ্যামিতিক হার গাণিতিক হারকে অতিক্রম করে চলে।
৪. জ্যামিতিক হার = √(2 × 4 × 8) = √64 = 8
এখানে, মৌলিক ঘটকগুলির গুণফল হচ্ছে 64 এবং তাদের সংখ্যা সমমান, তাহলে জ্যামিতিক হার হল 8।
অন্যদিকে, গাণিতিক হার = (5 + 10 + 15 + 20) / 4 = 50 / 4 = 12.5
এখানে, সমস্ত মানের যোগফল হচ্ছে 50 এবং তাদের সংখ্যা দ্বারা ভাগ করা হলে গাণিতিক হার হল 12.5।