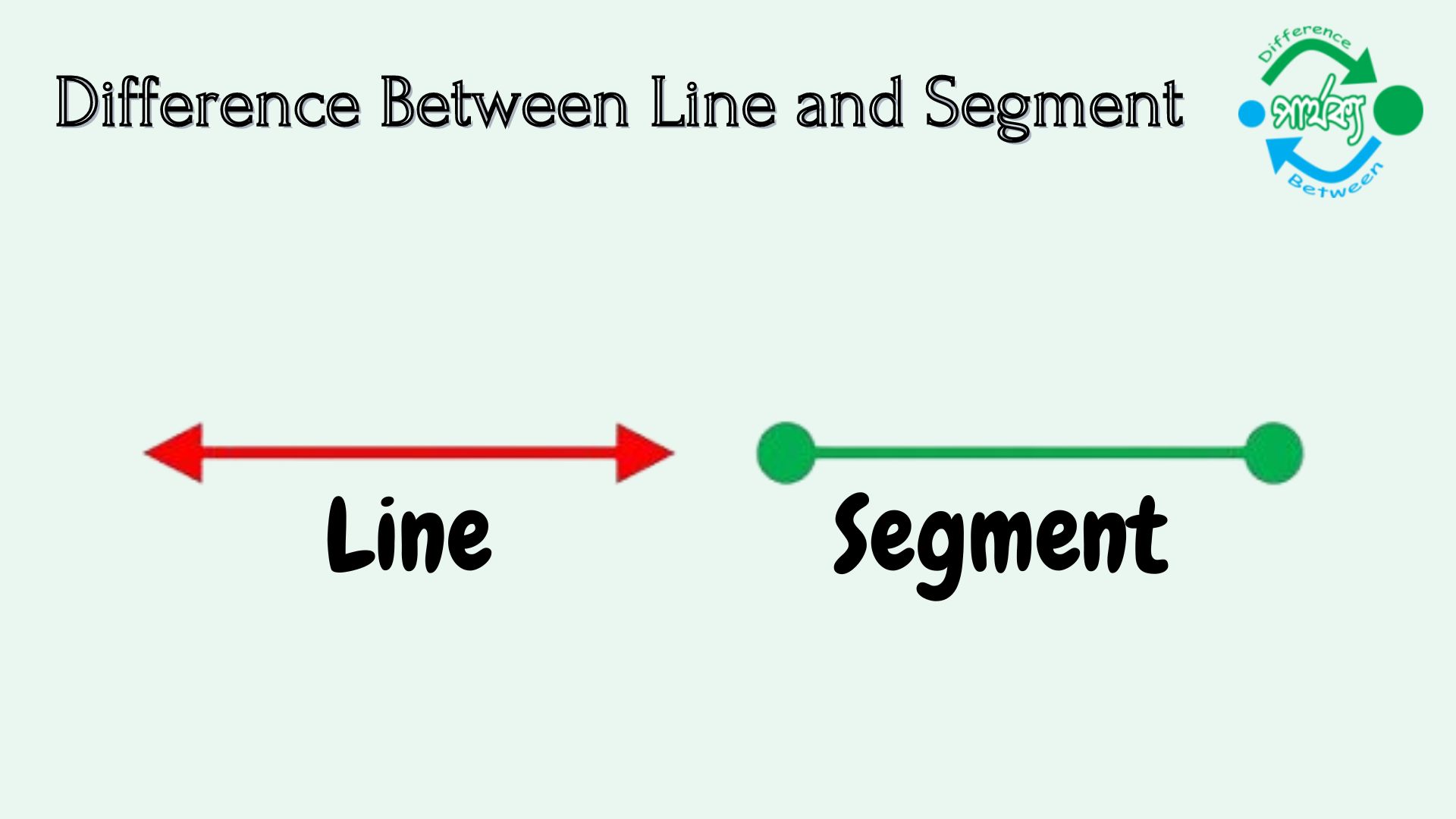
রেখা (Line) :
যার অসীম দৈর্ঘ্য আছে কিন্তু প্রস্থ ও বেধ বা উচ্চতা নেই তাকে রেখা (Line) বলে। অর্থাৎ রেখা হলো একাধিক বিন্দুর পারস্পরিক সংযোগের ফলে সৃষ্ট পথবিশেষ। অন্যভাবে বললে একটি বিন্দুর চলার পথকে রেখা বলা হয়। এই চলার পথটি যখন সোজা বা সরল হয়, তখন তাকে সরলরেখা বলা হয় আর যখন পথটা বাঁকা হয়, তখন যে পথটি সৃষ্টি হয় তাকে বলা হয় বক্ররেখা।
রেখার সাহায্যে বিভিন্ন ধরনের জ্যামিতিক আকার তৈরি করা যায়। যেমন: সরলরেখার সাহায্যে ত্রিভুজ, চতুর্ভুজ, আয়তক্ষেত্র, রম্বস, সামান্তরিক, পঞ্চভুজ, ষড়ভুজ ইত্যাদি তৈরি করা যায়। আবার, বক্ররেখার সাহায্যে তৈরি করা যায় বৃত্ত, উপবৃত্ত, অধিবৃত্ত, ইত্যাদি।
রেখাংশ (Segment) :
যার নির্দিষ্ট দৈর্ঘ্য ও দুইটি প্রান্তবিন্দু আছে তাকে রেখাংশ বলে। বা প্রকৃতপক্ষে রেখা হল কতগুলো বিন্দুর সমষ্টি। রেখার সীমাবদ্ধ অংশকে রেখাংশ (Parts of line) বলে। অন্যভাবে বলা যায়, জ্যামিতির ভাষায় রেখাংশ হলো কোনো রেখার এমন একটি অংশ বা খণ্ডাংশ যা ঐ রেখার উপর অবস্থিত দুটি স্বতন্ত্র প্রান্ত বিন্দুর মাধ্যমে আবদ্ধ এবং যেখানে রেখাটির এই বিন্দু দুটির মধ্যে থাকা প্রতিটি বিন্দুই উপস্থিত থাকে। রেখার এই স্বতন্ত্র বিন্দু দুটি যারা রেখাংশের সীমানা নির্ধারণ করে তাদেরকে রেখাংশের প্রান্তবিন্দু নামে অভিহিত করা হয়। একটি বদ্ধ রেখাংশ-এ এর উভয় প্রান্তবিন্দু অন্তর্ভুক্ত থাকে,
অপরদিক একটি খোলা রেখাংশ-এ এর উভয় প্রান্তবিন্দু অনুপস্থিত থাকে এবং একটি অর্ধ-খোলা রেখাংশ কেবল একটিই প্রান্ত বিন্দু ধারণ করে। জ্যামিতিতে রেখাংশকে সাধারণত প্রান্তবিন্দু দুটির জন্য ব্যবহৃত প্রতীকের উপরে একটি রেখা বা টান চিহ্ন দিয়ে সূচিত করা হয়।
রেখা ও রেখাংশের মধ্যে পার্থক্যঃ
রেখা থেকে রশ্মি এবং রশ্মি থেকে রেখাংশের উৎপত্তি হলেও এদের মধ্যে অনেকাংশে পার্থক্য রয়েছে। নিচে রেখা ও রেখাংশের মধ্যে পার্থক্য দেখানো হয়েছে-
১। যার অসীম দৈর্ঘ্য আছে কিন্তু প্রস্থ ও বেধ বা উচ্চতা নেই তাকে রেখা (Line) বলে। অন্যদিকে, যার নির্দিষ্ট দৈর্ঘ্য ও দুইটি প্রান্তবিন্দু আছে তাকে রেখাংশ বলে।
২। রেখার নির্দিষ্ট দৈর্ঘ্য নাই। অন্যদিকে, রেখাংশের নিদিষ্ট দৈর্ঘ্য আছে।
৩. রেখা সিমাহীন রেখাংশ। অন্যদিকে, দুইটি প্রান্ত বিন্ধু আছে। রেখাংশ সিমাবদ্ধ।
৪. অনির্দিষ্ট দৈর্ঘ্য বোঝাতে রেখা আকা হয়। অন্যদিকে, নির্দিষ্ট দৈর্ঘ্য বোঝাতে রেখাংশ আঁকা হয়।
৫. একটি রেখাকে দ্বিখণ্ডিত করলে দুটি রশ্মির উৎপত্তি হয়। অন্যদিকে, একটি রেখাংশকে দ্বিখণ্ডিত করলে দুটি নতুন রেখাংশের উৎপত্তি
হয়।
৬. একটি রেখাকে তিনটি খণ্ড করলে দুটি রশ্মি ও একটি রেখাংশের উৎপত্তি হয়। অন্যদিকে, একটি রেখাংশকে তিনটি খণ্ড করলে তিনটি নতুন রেখাংশের উৎপত্তি হয়।