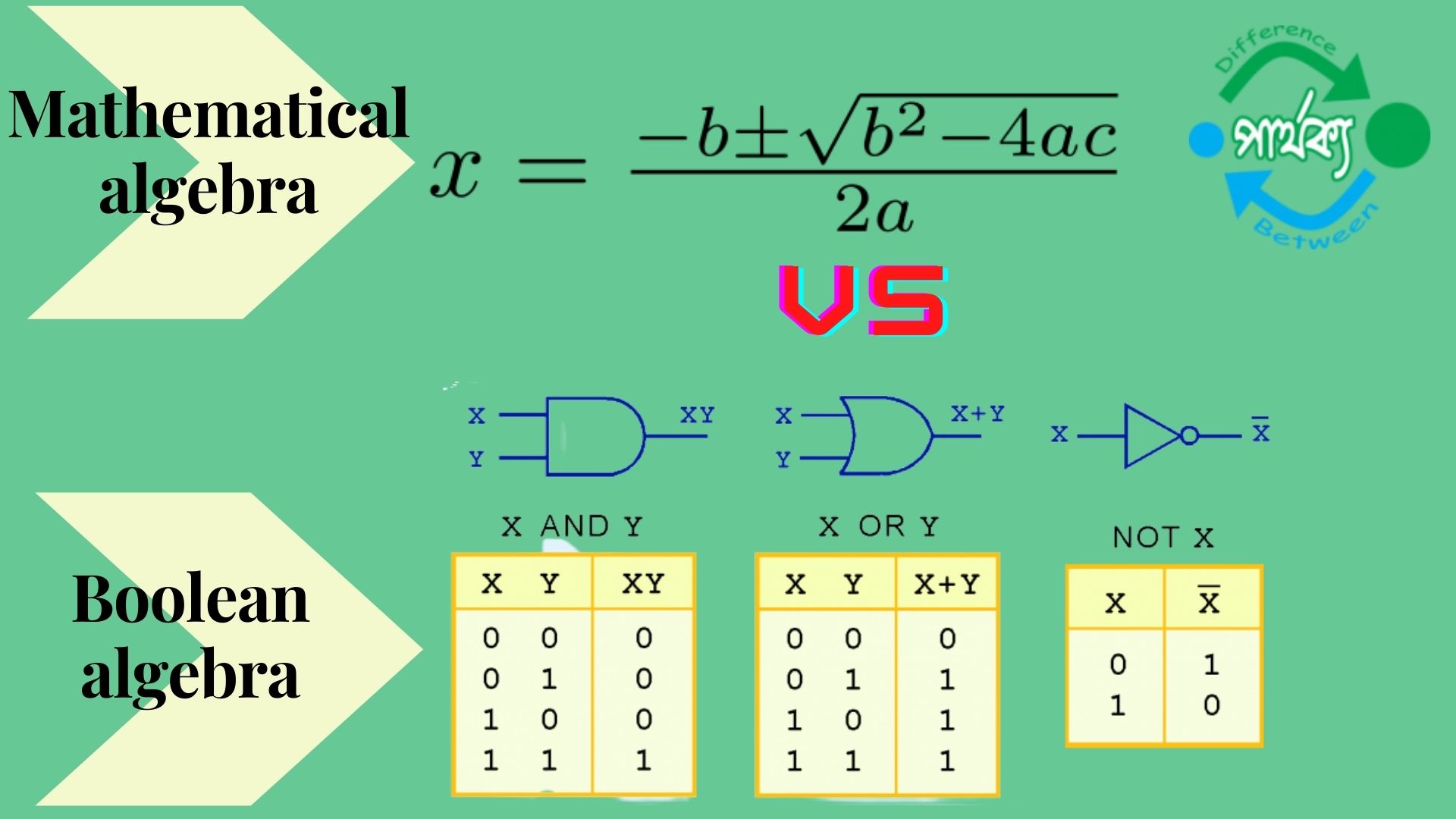
গাণিতিক বীজগণিত (Boolean algebra):
ব্যুৎপত্তিগতভাবে, বীজগণিত শব্দটি আরবি الجبر (আল-জাবর) যার অর্থ পুনরায় সংযুক্তি” বা “পুনরায় সংহতকরণ। বীজগণিত ব্যাবিলন এবং মিশরের সভ্যতা থেকে আসে, খ্রিস্টের আগে, তারা প্রথম এবং দ্বিতীয় ডিগ্রীর সমীকরণগুলি সমাধান করার জন্য এই পদ্ধতিটি ব্যবহার করেছিল। তারপরে প্রাচীন গ্রীসে অবিরত, গ্রীকরা সমীকরণ এবং উপপাদ্য প্রকাশ করতে বীজগণিত ব্যবহার করত। যেমন: পাইথাগোরিয়ান উপপাদ্য। সর্বাধিক প্রাসঙ্গিক গণিতবিদ ছিলেন আর্কিমিডিস, হেরেন এবং ডায়োপাঙ্কে। বালডোরের মতে, বীজগণিত হল গণিতের একটি শাখা যা সম্ভবত সবচেয়ে সাধারণভাবে বিবেচিত পরিমাণের অধ্যয়ন করে। এই অর্থে, এটি লক্ষ করা যায় যে কিউবার গণিতবিদ অরেলিও বাল্ডোরের একটি বই “বাল্ডোর বীজগণিত” রচনা দ্বারা বীজগণিতের শিক্ষার প্রাধান্য রয়েছে, যা এই বিজ্ঞানের সমস্ত অনুমানকে বিকাশ করে এবং পরিচালনা করে।
বুলিয়ান বীজগণিত (Mathematical algebra):
বুলিয়ান বীজগণিত (Boolean algebra) যা ১৮৪৭ সালে জর্জ বুল কর্তৃক তার বই চিন্তার নিয়ম নিয়ে কিছু চিন্তাভাবনা “এন ইনভেস্টিগেশান অফ দ্য লজ অফ থট” গ্রন্থে আবিষ্কৃত, হল সাধারণ বীজগণিতেরই একটি রকমফের। বুলিয়ান বীজগণিত তিনভাবে সাধারণ বীজগণিত থেকে ভিন্ন হতে পারে-চলকের মান গ্রহণে, যা সাংখ্যিক কোন চিহ্নের বদলে লজিক মেনে চলে, যথাক্রমে “1” এবং “0”; এই মানগুলোতে প্রযোজ্য অপারেশনে; এবং এই অপারেশনগুলোর বৈশিষ্ট্যে, অর্থাৎ তাদের নিয়মে। গাণিতিক যুক্তি, ডিজিটাল যুক্তি, গণকযন্ত্রের প্রোগ্রামিং, সেট তত্ত্ব এবং পরিসংখ্যানে বুলিয়ান বীজগণিতের ব্যবহার রয়েছে। বুলিয়ান বীজগণিতে মূলত তিনটি মৌলিক অপারেশন বা ক্রিয়া রয়েছে-যৌক্তিক যোগ,যৌক্তিক গুণ এবং পরিপূরক৷ ।
বুলিয়ান বীজগণিতে যৌক্তিক যোগ মানে সাধারণ বিবৃতিতে অথবা বোঝায়৷ যেমন – যদি বৃষ্টি হয় অথবা রাস্তা ভেজা থাকে তাহলে করিম যাবে৷ এখন রাস্তা ভেজা থাকলেই করিম যাবে৷ আবার বৃষ্টি হলেই করিম যাবে৷ দুটি শর্তের একটি সত্য হলেই করিম যাবে৷ বুলিয়ান বীজগণিতেে বক্তব্যটি হবে – a + b যেখানে বৃষ্টি হওয়ার চলক a এবং রাস্তা ভেজা থাকার চলক b
গাণিতিক বীজগণিত এবং বুলিয়ান বীজগণিতের মধ্যে পার্থক্য:
১। বীজগণিত শব্দটি আরবি الجبر (আল-জাবর) যার অর্থ পুনরায় সংযুক্তি” বা “পুনরায় সংহতকরণ। বীজগণিত ব্যাবিলন এবং মিশরের সভ্যতা থেকে আসে, খ্রিস্টের আগে, তারা প্রথম এবং দ্বিতীয় ডিগ্রীর সমীকরণগুলি সমাধান করার জন্য এই পদ্ধতিটি ব্যবহার করেছিল। অন্যদিকে বুলিয়ান বীজগণিত (Boolean algebra) যা ১৮৪৭ সালে জর্জ বুল কর্তৃক তার বই চিন্তার নিয়ম নিয়ে কিছু চিন্তাভাবনা “এন ইনভেস্টিগেশান অফ দ্য লজ অফ থট” গ্রন্থে আবিষ্কৃত, হল সাধারণ বীজগণিতেরই একটি রকমফের।
২। গণিতের কিছু ক্ষেত্র যা বিমূর্ত বীজগণিতের শ্রেণিবিন্যাসের আওতায় আসে তাদের নামে বীজগণিত শব্দটি রয়েছে; রৈখিক বীজগণিত এর একটি উদাহরণ। অন্যদের নামে অবশ্য বীজগণিত শব্দটি নেই : গ্রুপ তত্ত্ব, রিং তত্ত্ব এবং ক্ষেত্র তত্ত্ব তার উদাহরণ। অন্যদিকে বুলিয়ান বীজগণিতে মূলত তিনটি মৌলিক অপারেশন বা ক্রিয়া রয়েছে-যৌক্তিক যোগ,যৌক্তিক গুণ এবং পরিপূরক৷ ।
৩। বীজগণিত প্রতি গণিতের শাখা যেখানে ক্রম সংখ্যা, অক্ষর এবং চিহ্নগুলি ব্যবহার করে সাধারণ করা হয় যা প্রতীকীভাবে কোনও সংখ্যা বা অন্যান্য গাণিতিক সত্তাকে উপস্থাপন করে। অন্যদিকে ডিজিটাল সার্কিট বিশ্লেষন করার জন্য বুলিয়ান বীজগণিতেও 1 ও 0 এই দুটি অংক ব্যবহার করা হয়। দুই অংক বিশিষ্ট সংখ্যাপদ্ধতিকে বাইনারি সংখ্যাপদ্ধতি বলা হয়। তাই বুলিয়ান বীজগনিতের অপর নাম বাইনারি বীজগনিত।