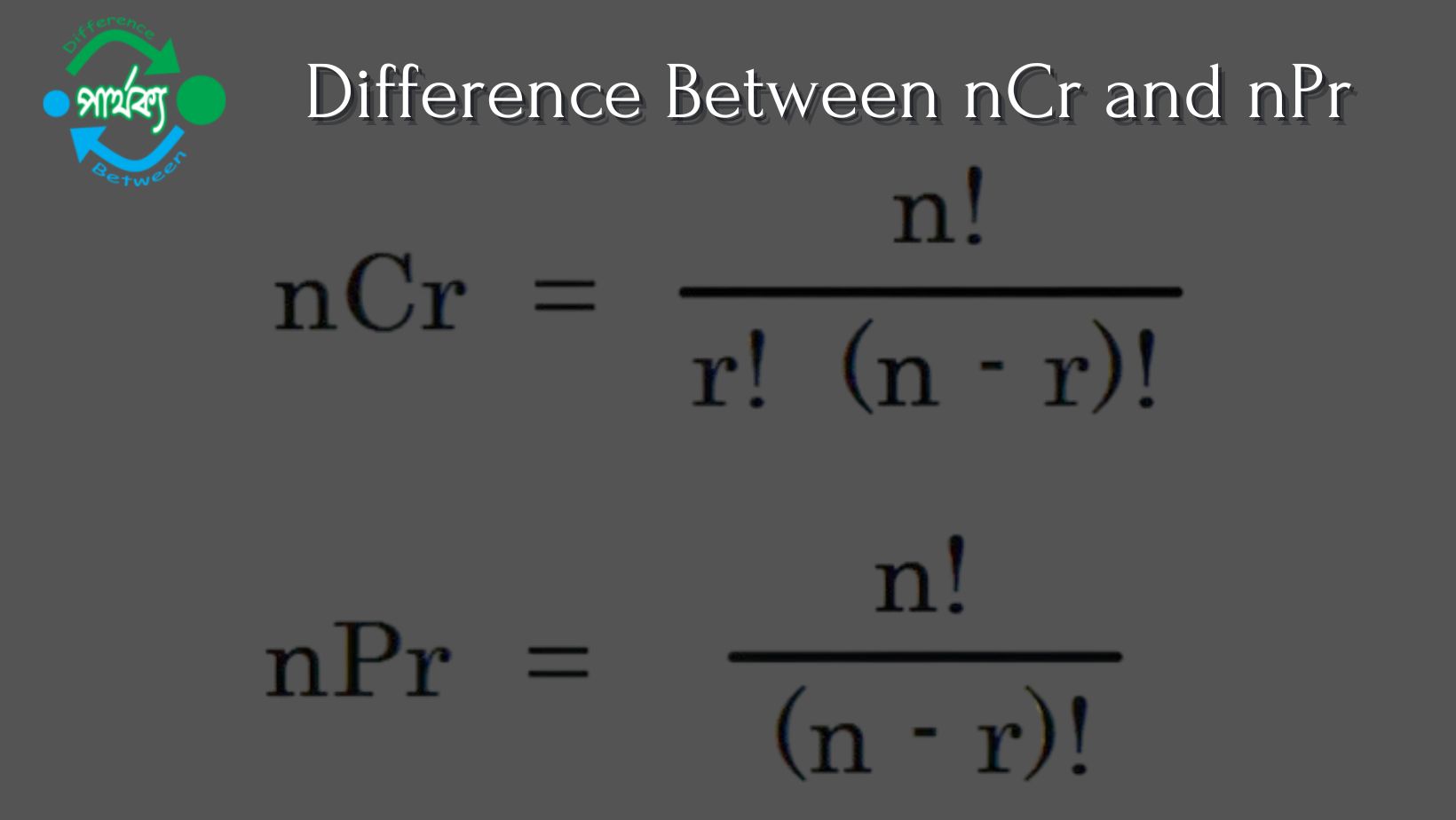গণিতে, nCr এবং nPr হল দুটি গুরুত্বপূর্ণ সম্ভাবনা বিশ্লেষণের সূত্র। এরা দুজনে একই পরিমাণের উপাদান থেকে বিভিন্ন বিন্যাস তৈরির সম্ভাবনা নির্ণয় করে। তবে, দুটি সূত্রের মধ্যে কিছু পার্থক্য রয়েছে। nCr ও nPr এর মধ্যে পার্থক্য নিচে দেখানো হয়েছে-

nCr :
nCr হল একটি সমাবেশ সূত্র। এটি নির্দিষ্ট ক্রমের বিন্যাস নির্ণয় করে। উদাহরণস্বরূপ, যদি আপনার কাছে পাঁচটি ভিন্ন রঙের বল থাকে এবং আপনি এগুলিকে একটি সারিতে সাজানোর চেষ্টা করেন, তাহলে nCr সূত্র আপনাকে বলগুলির কোন ক্রমটি সম্ভব তা নির্ধারণ করতে সাহায্য করবে।
সূত্র: nCr = n! / (r!(n-r)!)
যেখানে:
n হল উপাদানের সংখ্যা
r হল বিন্যাস করা উপাদানের সংখ্যা
n! হল n এর ফ্যাক্টরিয়াল

nPr :
nPr হল একটি বিন্যাস সূত্র। এটি ক্রম নির্বিশেষে বিন্যাস নির্ণয় করে। উদাহরণস্বরূপ, যদি আপনার কাছে পাঁচটি ভিন্ন রঙের বল থাকে এবং আপনি এগুলিকে একটি ঝুড়িতে ফেলে দেওয়ার চেষ্টা করেন, তাহলে nPr সূত্র আপনাকে বলগুলির কোন বিন্যাসটি সম্ভব তা নির্ধারণ করতে সাহায্য করবে।
সূত্র: nPr = n! / (n-r)!
যেখানে:
n হল উপাদানের সংখ্যা
r হল বিন্যাস করা উপাদানের সংখ্যা
n! হল n এর ফ্যাক্টরিয়াল

nCr ও nPr এর মধ্যে পার্থক্যঃ
nCr হল একটি সমাবেশ সূত্র। এটি নির্দিষ্ট ক্রমের বিন্যাস নির্ণয় করে। উদাহরণস্বরূপ, যদি আপনার কাছে পাঁচটি ভিন্ন রঙের বল থাকে এবং আপনি এগুলিকে একটি সারিতে সাজানোর চেষ্টা করেন, তাহলে nCr সূত্র আপনাকে বলগুলির কোন ক্রমটি সম্ভব তা নির্ধারণ করতে সাহায্য করবে।

অন্যদিকে, nPr হল একটি বিন্যাস সূত্র। এটি ক্রম নির্বিশেষে বিন্যাস নির্ণয় করে। উদাহরণস্বরূপ, যদি আপনার কাছে পাঁচটি ভিন্ন রঙের বল থাকে এবং আপনি এগুলিকে একটি ঝুড়িতে ফেলে দেওয়ার চেষ্টা করেন, তাহলে nPr সূত্র আপনাকে বলগুলির কোন বিন্যাসটি সম্ভব তা নির্ধারণ করতে সাহায্য করবে।

কতগুলো দ্রব্য থেকে প্রতিবারে কয়েকটি বা সবগুলোকে প্রতিবার নিয়ে যতগুলো দল গঠন করা যায় তাদের প্রত্যেকটিকে এক একটি সমাবেশ বা Combination বলে। সমাবেশের ক্ষেত্রে একই দলের অন্তর্ভুক্ত বলে অন্তর্ভুক্ত সদস্যদের বা দ্রব্যগুলোর ক্রম উপেক্ষা করা হয়ে থাকে। ধরি, ক, খ, গ তিনটি অক্ষর। তিনটি থেকে প্রতিবারে ২টি করে নিয়ে যদি দল গঠন করা হয় তাহলে তিনটি দল পাওয়া যায়। যথাক্রমে, কখ/খক, খগ/গখ ও গক/কগ। এই বিষয়টিকে nCr গাণিতিকভাবে রুপে প্রকাশ করা হয়। এখানে n দ্রব্য সংখ্যা, C সমাবেশ সম্পর্কিত একটি মাধ্যম এবং r হলো প্রতিবারে যতগুলো দ্রব্য নিয়ে সমাবেশ গঠিত হচ্ছে তার সংখ্যা।

মোটের উপর, nCr = n! / (r!(n-r)!) এখানে n! হলো ১x২x৩x…….n এবং r! হলো ১x২x৩x………r.

অন্যদিকে, বিন্যাস এর অর্থ সাজানো। কয়েকটি দ্রব্য থেকে কিছু সংখ্যক দ্রব্য নিয়ে বা সব কয়টি দ্রব্য একত্রে নিয়ে বিভিন্ন উপায়ে সাজালে এর এক একটিকে বিন্যাস বলে। ধরি, ক, খ, গ এই তিনটি অক্ষর হতে প্রতিবার একটি করে নিয়ে সাজালে ক, খ, গ এই তিনটি উপায়ে সাজানো যায় এবং এই সাজানোটাই হলো বিন্যাস। আবার ২টি করে নিলে কখ, খগ, গক, কগ, খক, গখ এই ৬টি উপায়ে সাজানো যায়। সবগুলো নিয়ে সাজালে কখগ, কগখ, গকখ, গখক, খকগ, খগক এই ছয়টি উপায়ে সাজানো যায় এবং এধরনের সাজানোর এক একটি হলো বিন্যাস। প্রকৃতপক্ষে, nPr = n! / (n-r)! যেখানে r প্রতিটি বিন্যাসের আকার অর্থাৎ মূল উপাদান সেট থেকে প্রতিবার ঠিক কতটি উপাদান নিয়ে প্রতিটি বিন্যাস গঠিত হচ্ছে তার সংখ্যা, এবং n সেই সেটের আকার যা থেকে বিন্যাসের উপাদান গৃহীত হয়।