সম্ভাবনা অপেক্ষক (Probability function):

কোন বিচ্ছিন্ন চলক X এর যে কোন মান x ঘটার সম্ভাবনা যদি f(x) হয় তহলে f(x) কে X এর সাথে সংশ্লিষ্ট সম্ভাবনা অপেক্ষক বলে। আবার f(x) কে সম্ভাবনা অপেক্ষক বলা হবে যদি উহা নিম্নরূপ শর্ত মেনে চলে। যথা:

(i) সমস্ত ঘটনা X এর জন্য f(x)≥০ (ii)

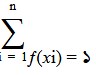
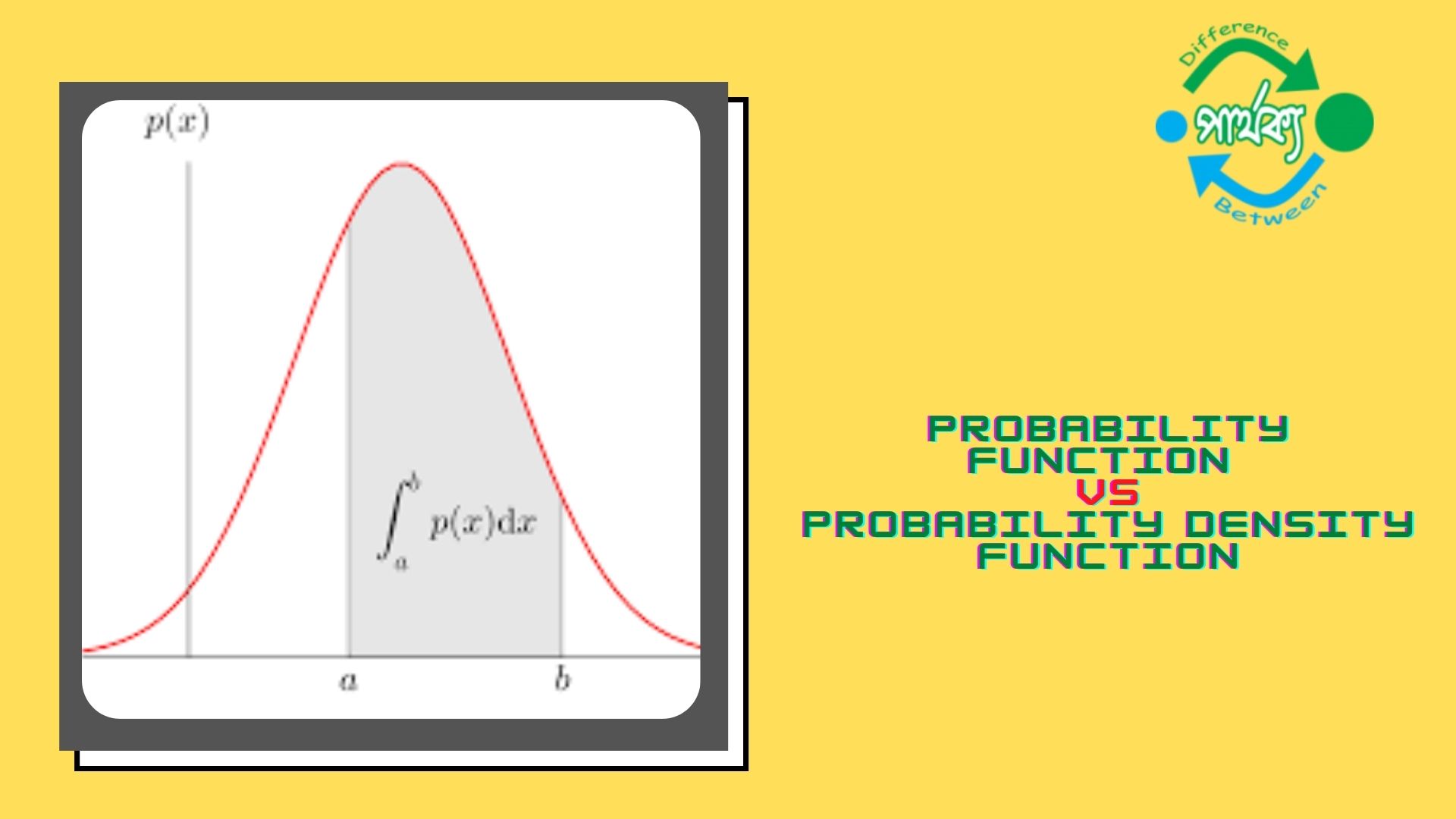
সম্ভাবনার ঘনত্ব অপেক্ষক (Probability density function):

অবিচ্ছিন্ন দৈব চলকের ক্ষেত্রে সম্ভাবনা ঘনত্ব অপেক্ষক হয়। মনে করি X একটি অবিচ্ছিন্ন দৈব চলক যার কোন নির্দিষ্ট মানের জন্য সম্ভাবনা পাওয়া যাবে না কিন্তু এর মান কোন নির্দিষ্ট পরিসীমা A এবং B এর মধ্যে থাকার সম্ভাবনা পাওয়া যাবে এবং একে f(x) d(x) দ্বারা প্রকাশ করা হয়। f(x) d(x) কে সম্ভাবনা ঘনত্ব অপেক্ষক (Probability density function) বা P.d.f বলা হয়।

সম্ভাবনা অপেক্ষক এবং সম্ভাবনার ঘনত্ব অপেক্ষকের মধ্যে পার্থক্য:

কোন বিচ্ছিন্ন চলক X এর যে কোন মান x ঘটার সম্ভাবনা যদি f(x) হয় তহলে f(x) কে X এর সাথে সংশ্লিষ্ট সম্ভাবনা অপেক্ষক বলে। সম্ভাবনা অপেক্ষক এবং সম্ভাবনার ঘনত্ব অপেক্ষকের মধ্যে পার্থক্য নিম্নরূপ-

১। কোন বিচ্ছিন্ন চলক X এর যে কোন মান x ঘটার সম্ভাবনা যদি f(x) হয় তহলে f(x) কে X এর সাথে সংশ্লিষ্ট সম্ভাবনা অপেক্ষক বলে। অন্যদিকে কোন নির্দিষ্ট পরিসীমা A এবং B এর মধ্যে থাকার সম্ভাবনা পাওয়া যাবে এবং একে f(x) d(x) দ্বারা প্রকাশ করা হয়। f(x) d(x) কে সম্ভাবনা ঘনত্ব অপেক্ষক (Probability density function) বা P.d.f বলা হয়।

২। সম্ভবনা অপেক্ষক p(x) দ্বারা প্রকাশ করা হয়। অন্যদিকে সম্ভবনা ঘনত্ব অপেক্ষক f(x) দ্বারা প্রকাশ করা হয়।

৩। সম্ভবনা অপেক্ষক দুটি শর্ত মেনে চলে যথা- (i) p(x)≥0 (ii) p(x)= 1 অন্যদিকে সম্ভবনা ঘনত্ব অপেক্ষক দুটি শর্ত মেনে চলে (i) f(x)≥0
(ii) f(x) dx=1

৪। সম্ভবনা অপেক্ষকের উদাহরণ হল-দ্বিপদী ও পৈসু বিন্যাস। অন্যদিকে সম্ভবনা ঘনত্ব অপেক্ষকের উদাহরণ হল-পরিমিতি বিন্যাস।