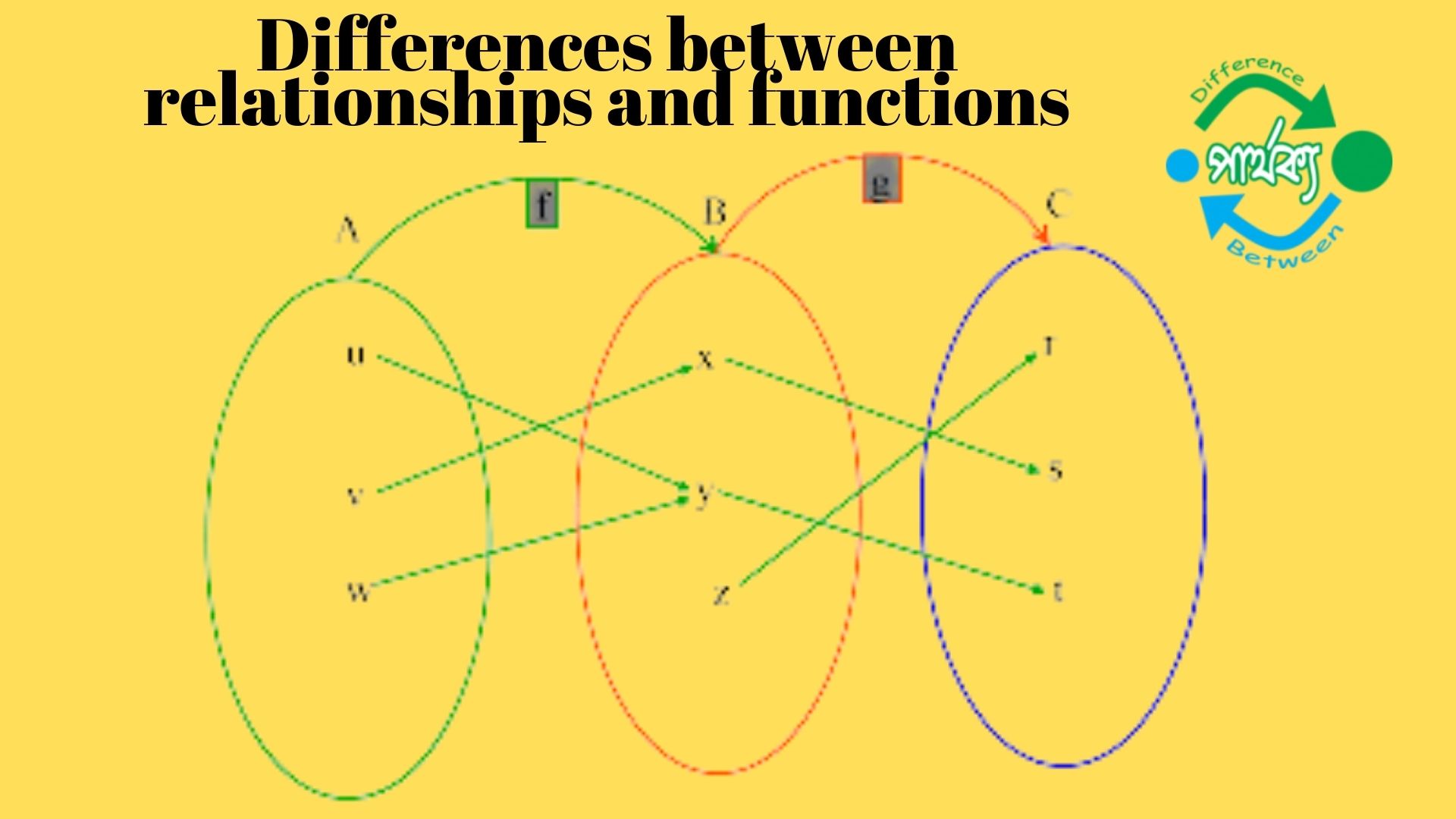
অন্বয় (Relations):
যা দ্বারা দুই বা ততোধিক চলকের মধ্যে অথবা, দুইটি সেটের মধ্যে সম্পর্ক বুঝানো হয় তাকে অন্বয় বলে। অথাৎ A ও B সেট হলে A×B এর কোন অশূণ্য উপসেটকে A থেকে B তে একটি অন্বয় বলা হয় । অর্থাৎ যদি S, A থেকে B তে একটি অন্বয় হয় তবে, S = {(x,y) ∣ x ∈ A, y ∈ B}
আবার, A×A এর কোন অশূণ্য উপসেটকে A সেটে একটি অন্বয় বলে ।
ফাংশন (Function):
ফাংশন হল বিশেষ ধরনের অন্বয়। কোনো অন্বয়ে অবস্থিত ক্রমজোড়ের প্রথম উপাদানগুলি ভিন্ন ভিন্ন হলে ঐ অন্বয়কে ফাংশন বলে। অন্যভাবে বলা যায় যে, যদি কোন অন্বয়ে একই প্রথম উপাদানবিশিষ্ট একাধিক ক্রমজোড় না থাকে, তবে ঐ অন্বয়কে ফাংশন বলে। অর্থাৎ, A ও B সেট হলে A থেকে B সেটে ফাংশন F হচ্ছে A×B এর এমন একটি উপসেট যেন-
১. প্রতি a ∈ A এর জন্য একটি উপাদান b ∈ B থাকে যেখানে (a,b) ∈ F
২.যদি (a,b) ∈ F হয় এবং (a,b′) ∈ F হয় তবে অবশ্যই b = b′ হবে ।
F, A থেকে B সেটে ফাংশন হলে তাকে F : A= B লিখে প্রকাশ করা হয় । (x,y) ∈ F হলে, y কে F এর অধীনে x এর ছবি (Image) বলা হয় এবং y = F(x) লেখা হয়।
অন্বয় ও ফাংশন এর মধ্যে পার্থক্য:
যদি কোন অন্বয়ে একই প্রথম উপাদানবিশিষ্ট একাধিক ক্রমজোড় না থাকে, তবে ঐ অন্বয়কে ফাংশন বলে। অন্বয় ও ফাংশন এর মধ্যে পার্থক্য নিচে আলোচনা করা হয়েছে-
১। যা দ্বারা দুই বা ততোধিক চলকের মধ্যে অথবা, দুইটি সেটের মধ্যে সম্পর্ক বুঝানো হয় তাকে অন্বয় বলে। অন্যদিকে যদি কোন অন্বয়ে একই প্রথম উপাদানবিশিষ্ট একাধিক ক্রমজোড় না থাকে, তবে ঐ অন্বয়কে ফাংশন বলে।
২। প্রত্যেক ফাংশন একটি অন্বয় কিন্তু প্রত্যেক অন্বয় ফাংশন নাও হতে পারে।
৩। কোনো অন্বয় ফাংশন হবে যদি তা নিম্নোক্ত দুইটি শর্ত মেনে চলে। যথা : যদি X ও Y দুইটি সেট হয় এবং F: X→Y দ্বারা নির্দেশিত হয় তাহলে F ফাংশন হবে যদি নিম্নোক্ত শর্তদ্বয় পূরণ করে।
(i) X এর প্রত্যেকটি উপাদান অবশ্যই Y এর সাথে সম্পর্কিত হতে হবে।
(ii) X এর প্রত্যেকটি উপাদান Y এর একাধিক উপাদানের সাথে সম্পর্ক করতে পারবে না। কিন্তু X এর একাধিক উপাদান Y এর একটি উপাদানের সাথে সম্পর্ক করতে বাধা নেই।
৪। S এ অন্তর্ভুক্ত ক্রমজোড়গুলোর প্রথম উপাদানসমূহের সেটকে S এর ডোমেন এবং দ্বিতীয় উপাদানসমূহের সেটকে S এর রেঞ্জ বলা হয় । S এর ডোমেনকে ডোম S এবং রেঞ্জকে রেঞ্জ S লিখে প্রকাশ করা হয় । অর্থাৎ, ডোম S = {x ∣ x ∈ A, (x,y) ∈ S}। অন্যদিকে F : A→B এর ক্রমজোড়গুলোর প্রথম উপাদানসমূহের সেটকে F এর ডোমেন বলে যাকে ডোম F লিখে প্রকাশ করা হয় । অন্য কথায়, A কে F এর ডোমেন বলে। ডোম F = {x ∣ x ∈ A}